JavaPlex Tutorial
This article was originally written by Michael Bleher for the STRUCTURES Wiki (captured October 2025).
In this tutorial we will learn how to use the JavaPlex package in Matlab. For a more complete picture of JavaPlex please visit the projects homepage and consider also reading the tutorial provided there.
Installation
To use JavaPlex with Matlab you will need a working version of Matlab. Furthermore, JavaPlex requires Java version number 1.5 or higher. You can check your Java version in Matlab by entering version -java
To install JavaPlex in Matlab go to the latest release at . Download the zip file of matlab examples, named something like matlab-examples-4.3.4.zip. Unzip the folder to a known location, by default the resulting folder is called matlab_examples.
In Matlab, change your current folder to matlab_examples. Run the script load_javaplex.m that resides in this folder and import the JavaPlex routines provided by the package. You can do this by entering the following commands into the command line
load_javaplex.m; import edu.stanford.math.plex4.*;
You will need to reload the package with these commands every time you open a new Matlab session.
To check wether JavaPlex was loaded correctly, e.g. enter api.Plex4.createExplicitSimplexStream() which will return something like
ans = edu.stanford.math.plex4.streams.impl.ExplicitSimplexStream@513fd4
Basic constructions
Simplex Streams
JavaPlex implements abstract simplicial complexes via simplex streams, which are provided by the function
api.Plex4.createExplicitSimplexStream()
To a simplex stream we assign vertices and higher simplices as exemplified below.
Example: 1-sphere
In order to build a simplicial complex by hand, we first load the relevant function onto our target object
complex = api.Plex4.createExplicitSimplexStream();
and pass the vertices of the complex to it:
complex.addVertex(0); complex.addVertex(1); complex.addVertex(2);
In general a complex will have higher simplicies, which by definition are sets of vertices. These are added to the simplicial complex by similarly passing sets to the stream.
complex.addElement([0, 1]); complex.addElement([0, 2]); complex.addElement([1, 2]);
Once all simplices have been put into the stream, we close it by calling
complex.finalizeStream();
At this point complex is a simplicial complex that encodes the boundary of a triangle. We can get the number of simplices (of all dimension) contained in the simplicial complex by calling
complex.getSize()
Modular Simplicial Algorithm
For a given simplicial complex X, the function api.Plex4.getModularSimplicialAlgorithm(d, p) provides an algorithm that can calculate the persistence module of homology groups H_i(X,\mathbb{Z}/p\mathbb{Z}) for all i\leq d, together with representatives of the classes [x]\in H_i .
Note: This algorithm is used more generally for filtered complexes as discussed below. Every simplicial complex X is trivially filtered by \mathcal{F}_t(X) = X for all t \in \mathbb{R}.
Example: 1-sphere
Continuing our example from above, the homology groups over \mathbb{Z}/2\mathbb{Z} of complex up to dimension 3 can be extracted via
homology = api.Plex4.getModularSimplicialAlgorithm(3, 2); persistenceIntervals = homology.computeIntervals(complex)
The output is a number of intervals, that tell us for which values of the filtration parameter a non-trivial homology class exists. If we are also interested in representatives of the non-trivial classes we can use
persistenceAnnotatedIntervals = homology.computeAnnotatedIntervals(complex)
This gives the parameter values of non-trivial classes together with their representatives.
Example: n-sphere The explicit construction above is of course too tiresome for more complicated simplicial complexes. We exemplify which additional methods of simplex stream objects exist, by constructing n-spheres.
% set dimension and load simplex stream dimension = 9; sphere = api.Plex4.createExplicitSimplexStream();
% construct simplicial sphere stream.addElement(0:(dimension + 1)); stream.ensureAllFaces(); stream.removeElementIfPresent(0:(dimension + 1)); stream.finalizeStream();
% print out the total number of simplices in the complex stream.getSize()
% get homology algorithm over Z/2Z up to dimension+1 persistence = api.Plex4.getModularSimplicialAlgorithm(dimension + 1, 2);
% compute and print the homology groups intervals = persistence.computeIntervals(stream)
Filtered Chain Complexes
Generating Barcodes
Customization
Examples
We can now use what we’ve learned above to investigate more complicated data sets.
Periodic Helix
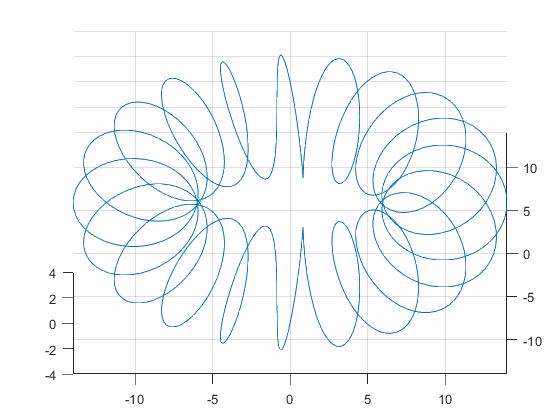
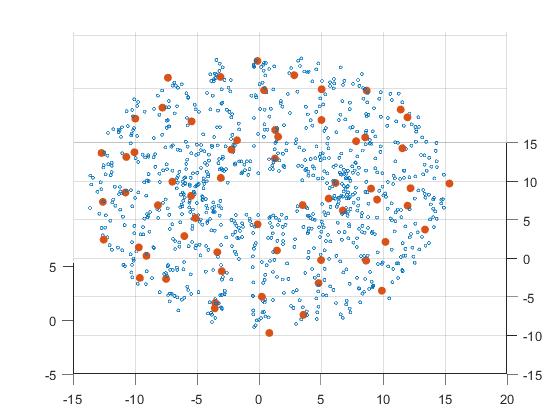
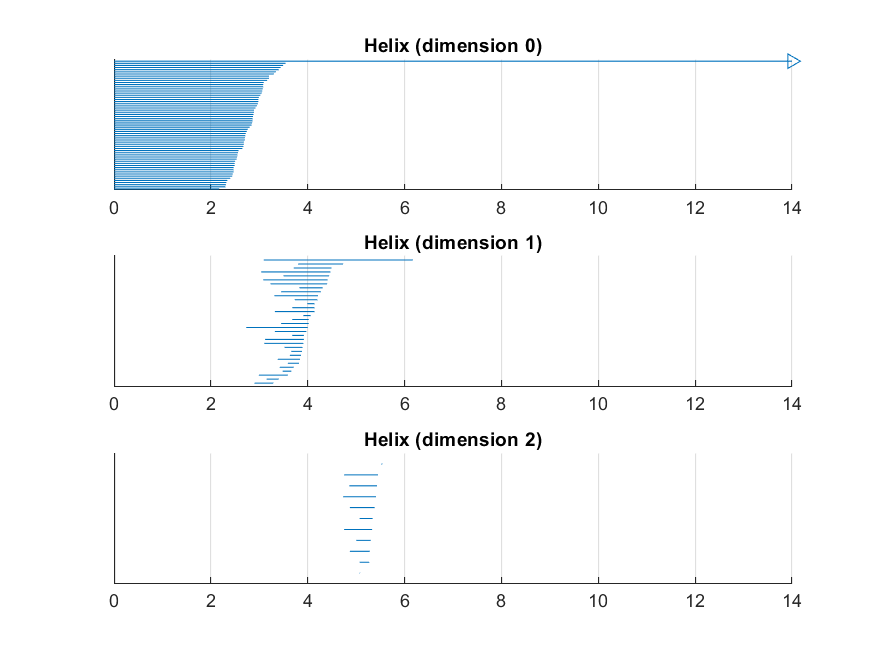
In this example we investigate a point cloud that arises from a one-dimensional underlying manifold, that is embedded in three dimensions in the form of a helix wound around a torus. The point cloud is generated from the one-dimensional embedded helix with noise.
import edu.stanford.math.plex4.*;
% define the point cloud of a Helix on a Torus R=10; r=4; n=20; t=[0:10^-3:1];
variancePercentage = 0.07; varianceScale = (r+R)*0.1;
x= (R+rcos(2pint)).cos(2pit)+varianceScalerand([1,10^3+1]); y= (R+rcos(2pint)).sin(2pit)+varianceScalerand([1,10^3+1]); z= rsin(2pint)+varianceScale*rand([1,10^3+1]); HelixPoints = [x(:),y(:),z(:)];
scatter3(HelixPoints(:,1),HelixPoints(:,2),HelixPoints(:,3),5) hold on
% build simplicial complex via LazyWitness with the following parameters max_dimension = 3; num_landmark_points = 65; max_filtration_value = (R+r); nu = 0; num_divisions = 1400;
% create a sequential maxmin landmark selector landmark_selector = api.Plex4.createMaxMinSelector(HelixPoints, num_landmark_points);
p = landmark_selector.getLandmarkPoints; NumberOfLandmarks = size(p) MaxDistanceToLandmarks = landmark_selector.getMaxDistanceFromPointsToLandmarks()
scatter3(HelixPoints(p,1),HelixPoints(p,2),HelixPoints(p,3),’filled’) hold off
% create a lazy witness stream stream = streams.impl.LazyWitnessStream(landmark_selector.getUnderlyingMetricSpace(), landmark_selector, max_dimension, max_filtration_value, nu, num_divisions); stream.finalizeStream()
% print out the size of the stream num_simplices = stream.getSize()
% get persistence algorithm over Z/2Z persistence = api.Plex4.getModularSimplicialAlgorithm(max_dimension, 2); intervals= persistence.computeIntervals(stream)
% create the barcode plots options.filename = ‘Helix’; options.max_filtration_value = max_filtration_value; options.max_dimension = max_dimension - 1; plot_barcodes(intervals, options);
The output of our analysis is depicted on the right. First of all we see that the point cloud seems to be supported on a torus. Furthermore one might argue that there is more structure in the data, but it is not obvious that the underlying manifold is a helix. Remarkably, the barcode tells us that there is a relatively long-lived 1-dimensional homology class, which suggests that the underlying manifold has one-dimensional origin. Contrary to expectation it is hard to argue that there is also a torus in the picture.
Cyclooctane Configuration Space
This example is taken from section 6 of the JavaPlex tutorial. It shows the calculation of persistent homology from a point sample of cyclo-octane configuration space.
import edu.stanford.math.plex4.*;
load pointsCycloOctane.mat size(pointsCycloOctane)
max_dimension = 3; num_landmark_points = 100; max_filtration_value = 0.6; nu = 1; num_divisions = 1000;
% create a sequential maxmin landmark selector landmark_selector = api.Plex4.createMaxMinSelector(pointsCycloOctane, num_landmark_points); R = landmark_selector.getMaxDistanceFromPointsToLandmarks()
% create a lazy witness stream stream = streams.impl.LazyWitnessStream(landmark_selector.getUnderlyingMetricSpace(), landmark_selector, max_dimension, max_filtration_value, nu, num_divisions); stream.finalizeStream()
% print out the size of the stream num_simplices = stream.getSize()
% get persistence algorithm over Z/2Z persistence = api.Plex4.getModularSimplicialAlgorithm(max_dimension, 2);
% compute the intervals intervals = persistence.computeIntervals(stream);
% create the barcode plots options.filename = ‘lazyCycloOctane’; options.max_filtration_value = max_filtration_value; options.max_dimension = max_dimension - 1; plot_barcodes(intervals, options);